Universal Turing Machines, Part 2: The encoding and overall design

2007/06/20 · by · in Comp*

The encoding for a machine with any number of states and any number of symbols:

Each state and each symbol will be numbered in binary, all the numbers must be padded to the same length. So, we can have symbols that number from 000 to 100, and states that number from 0010 to 1100.

Firstly, this UTM requires a register at the beginning of the tape that will be used for storing state information. Initially it can be filled with any number we want, as long as it is filled to the appropriate number of digits, and begins with a q.

q0000

Then we name the blank symbol. This can be any number, by convention, I’ve used the number 0. All symbols in the simulated machine must be padded to the same length. This symbol will be used to append to the tape every time the simulated machine tries to run off the right end of its tape.

B000

Then we specify the transition function for each symbol. qY and qX specify accept and reject states. The TM that recognizes (01)* is given by the transition table:
\begin{tabular}{c|ccc} &0&1&b\\ \hline $\boldsymbol{q_1}$&0,R,$\boldsymbol{q_2}$&1,R,reject&1,R,$\boldsymbol{q_3}$\\ $\boldsymbol{q_2}$&0,R,reject&1,R,$\boldsymbol{q_1}$&b,R,reject\\ $\boldsymbol{q_3}$&0,R,accept&1,R,accept&b,R,accept\\ \end{tabular}
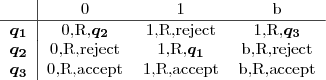
Thus, if we use B11 for the blank, and number everything else normally, this table becomes the encoded string:

Q01 S00Rs00q10 S01Rs01qX S11Rs01q11
Q10 S00Rs00qX S01Rs01q01 S11Rs11qX
Q11 S00Rs00qY S01Rs01qY S11Rs11qY

After this comes the input tape, which we mark with a T, so for 010101 we would get:
Ts00s01s00s01s00s01

Bringing that all together, by removing spaces and putting in the register and blank symbol, we end up with:
q01B11Q01S11Rs01q11S00Rs00q10S01Rs01qXQ10S11Rs11qXS00Rs00qXS01Rs01q01Q11S11Rs11qYS00Rs00qYS01Rs01qYTs00s01s00s01s00s01
where the overlines indicate the starting symbol and the position on the simulated tape.

The general procedure will be to:

  1. check that a symbol ion the tape is marked, if not copy the blank symbol onto the end, and make it the current symbol.
  2. find the part of the state diagram that corresponds to the symbol on the tape.
  3. update the symbol on the tape
  4. move the tape left or right one symbol
  5. copy the transition state to the register, unless it’s a qY or qX in which case we can Halt on accept or reject.
  6. find the function definition that corresponds to the state in the register and mark it for the next step of simulation
  7. repeat